trigonometri
Identitas trigonometri
Penjumlahan
Rumus sudut rangkap dua
Rumus sudut rangkap tiga
Rumus setengah sudut
 Sekan (lambang: sec; bahasa Inggris: secant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak pada sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi sekan di atas maka nilai sekan adalah
Sekan (lambang: sec; bahasa Inggris: secant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak pada sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi sekan di atas maka nilai sekan adalah  Hubungan sekan dengan kosinus:
Hubungan sekan dengan kosinus: 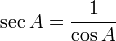 Kosekan (disimbolkan dengan cosec atau csc; bahasa Inggris: cosecant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kosekan di atas maka nilai kosekan adalah
Kosekan (disimbolkan dengan cosec atau csc; bahasa Inggris: cosecant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kosekan di atas maka nilai kosekan adalah  Hubungan kosekan dengan sinus:
Hubungan kosekan dengan sinus:  Kotangen (lambang: cot, cotg, atau cotan; bahasa Inggris: cotangent) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kotangen di atas maka nilai kotangen adalah
Kotangen (lambang: cot, cotg, atau cotan; bahasa Inggris: cotangent) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kotangen di atas maka nilai kotangen adalah  berikut Tabel sudut-sudut istimewa/Trigonometrinya.. => Tabel Sudut Istimewa
=> Tabel TrigonometrinyaSekarang, untuk memahami dan menghafalkan sudut-sudut trigonometri, kita harus hafal dulu tabel sudut-sudut istimewa diatas. Kalo sudah, sekarang kita pahami konsep kuadran I, II, III dan IV Pada kuadran I (0 – 90) , semua nilai sin, tan dan cos bernilai positif —> “semua” Pada kuadran II (90 – 180) , hanya sin bernilai positif —> sin dibaca “sindikat” Pada kuadran II (180 – 270) , hanya tan bernilai positif —> tan dibaca “tangan” Pada kuadran II (270 – 360) , hanya cos bernilai positif —>cos dibaca “kosong” Jadi, untuk mengingat gambar diatas hafalkan kalimat : “Semua Sindikat Tangannya Kosong” contoh 1 : Hitunglah nilai cos 210 ? cos 210 —-> berada dikuadran III —-> pasti negatif, jadi jawaban harus negatif cos 210 = cos (180 +30) = - cos 30 = -1/2√3 jadi nilai cos 210 = – 1/2 √3 (minus setengah akar tiga) contoh 2 : Hitunglah nilai sin 300 ? sin 300 —-> berada di kuadran IV —-> pasti negatif, jadi jawaban harus negatif sin 300 = sin (270 + 30) = – cos 30 = 1/2√3 jadi nilai sin 300 = – 1/2 √3 (minus setengah akar tiga) KONSEP nya : misalkan diketahui sudut sebesar x JIka kita merubah sudut x menjadi sudut y maka kita dapat menggunakan patokan pada nilai 90, 180, 270, dan 360. Misalnya sudut 210 = sudut (180 + 30) atau boleh juga sudut 210 = sudut (270 – 60), yang penting di ingat, kita harus merubah sudut tersebut sehingga mengandung sudut-sudut istimewa pada kuadran satu seperti 30, 45, 60, sehingga mudah untuk menghitungnya. Untuk Perubahan Sudut tadi ada hal yang terpenting untuk di pahami JIka kita menggunakan 90 dan 270 maka konsepnya “BERUBAH” sin berubah menjadi cos cos berubah menjadi sin tan berubah menjadi cotan Jika kita menggunakan 180 dan 360 maka konsepnya “TETAP” sin tetap menjadi sin cos tetap menjadi cos tan tetap menjadi tan contoh 3 : Hitung nilai sin 150 ? sin 150 —-> berada dikuadran II —-> pasti positif, jadi jawaban harus positif sin 150 = sin (90 + 60) = + cos 60 = +1/2 (positif setengah) —–> ingat sudut 90 KONSEP “BERUBAH” atau sin 150 = sin (180 – 30) = + sin 30 = +1/2 (positif setengah) —–> ingat sudut 180 KONSEP “TETAP” sumber
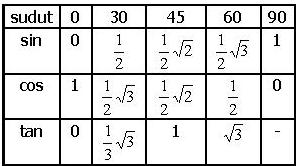
berikut Tabel sudut-sudut istimewa/Trigonometrinya.. => Tabel Sudut Istimewa
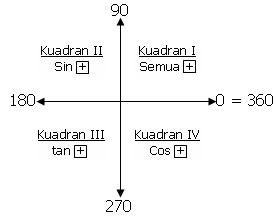
=> Tabel TrigonometrinyaSekarang, untuk memahami dan menghafalkan sudut-sudut trigonometri, kita harus hafal dulu tabel sudut-sudut istimewa diatas. Kalo sudah, sekarang kita pahami konsep kuadran I, II, III dan IV Pada kuadran I (0 – 90) , semua nilai sin, tan dan cos bernilai positif —> “semua” Pada kuadran II (90 – 180) , hanya sin bernilai positif —> sin dibaca “sindikat” Pada kuadran II (180 – 270) , hanya tan bernilai positif —> tan dibaca “tangan” Pada kuadran II (270 – 360) , hanya cos bernilai positif —>cos dibaca “kosong” Jadi, untuk mengingat gambar diatas hafalkan kalimat : “Semua Sindikat Tangannya Kosong” contoh 1 : Hitunglah nilai cos 210 ? cos 210 —-> berada dikuadran III —-> pasti negatif, jadi jawaban harus negatif cos 210 = cos (180 +30) = - cos 30 = -1/2√3 jadi nilai cos 210 = – 1/2 √3 (minus setengah akar tiga) contoh 2 : Hitunglah nilai sin 300 ? sin 300 —-> berada di kuadran IV —-> pasti negatif, jadi jawaban harus negatif sin 300 = sin (270 + 30) = – cos 30 = 1/2√3 jadi nilai sin 300 = – 1/2 √3 (minus setengah akar tiga) KONSEP nya : misalkan diketahui sudut sebesar x JIka kita merubah sudut x menjadi sudut y maka kita dapat menggunakan patokan pada nilai 90, 180, 270, dan 360. Misalnya sudut 210 = sudut (180 + 30) atau boleh juga sudut 210 = sudut (270 – 60), yang penting di ingat, kita harus merubah sudut tersebut sehingga mengandung sudut-sudut istimewa pada kuadran satu seperti 30, 45, 60, sehingga mudah untuk menghitungnya. Untuk Perubahan Sudut tadi ada hal yang terpenting untuk di pahami JIka kita menggunakan 90 dan 270 maka konsepnya “BERUBAH” sin berubah menjadi cos cos berubah menjadi sin tan berubah menjadi cotan Jika kita menggunakan 180 dan 360 maka konsepnya “TETAP” sin tetap menjadi sin cos tetap menjadi cos tan tetap menjadi tan contoh 3 : Hitung nilai sin 150 ? sin 150 —-> berada dikuadran II —-> pasti positif, jadi jawaban harus positif sin 150 = sin (90 + 60) = + cos 60 = +1/2 (positif setengah) —–> ingat sudut 90 KONSEP “BERUBAH” atau sin 150 = sin (180 – 30) = + sin 30 = +1/2 (positif setengah) —–> ingat sudut 180 KONSEP “TETAP” sumber











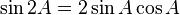







Tidak ada komentar:
Posting Komentar